L1-09 程序结构概述

程序结构概述

什么是程序结构

程序结构又叫结构化程序，渗透的是程序内部的思想逻辑。

比如你早晨起床有很多事情要干，先穿衣服，再洗脸刷牙，再吃早饭，再上学，这就是一个顺序结构，你在有顺序地做着一件一件事情。

而如果我们从一个月的角度看，每一天你都在做这些事情，那么这就是循环结构，重复做着同一些事情。

如果你每天要做的事情，是由一些前提条件决定的，比如冬天穿棉袄，夏天穿背心，那么这就是一个选择结构。

有了这些结构化的框架作为指引，我们写代码的时候思维会更加的清晰有条理。

结构化的程序设计便于理解、调试、修改，正确使用程序结构有利于设计出优秀的程序。

单选题

程序有（）种基本结构？

A. 2

B. 3

C. 4

题解

B，顺序、选择、循环3种基本结构

单选题

程序的结构不包括（    ）

A. 倒序结构

B. 顺序结构

C. 选择结构

D. 循环结构

题解

程序结构有：顺序结构、选择结构、循环结构

基本程序结构

基本的程序结构有三种：顺序结构，选择结构，循环结构。后面我们将一一讲解。

顺序结构

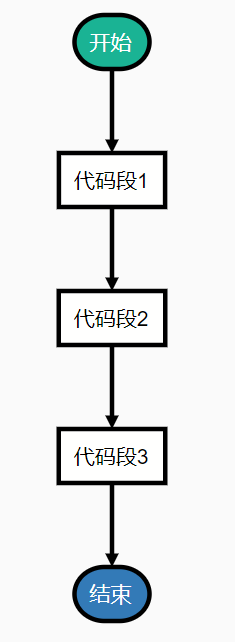
顺序结构是所有结构中最简单的一种，按照所写语句顺次执行即可。

2020 年 7 月 23 日，“天问一号” 火星探测器在中国文昌航天发射场点火升空，飞向火星。

火星探测的流程大概包含：

• 点火升空
• 开展探测任务
• 运抵文昌发射场
• 环绕火星飞行
• 着陆火星
• 到达火星预定轨道

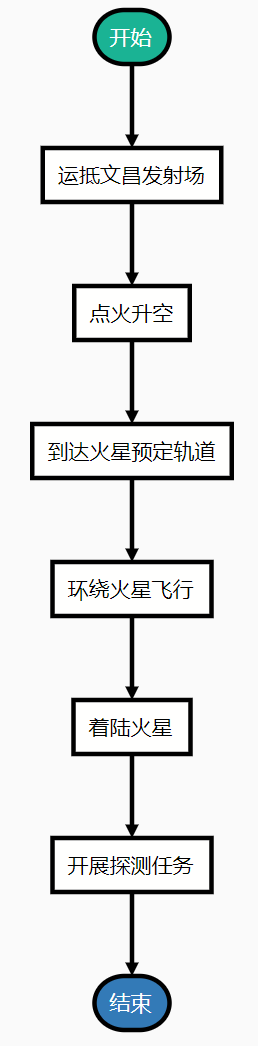
这就是一个典型的顺序结构。

选择结构

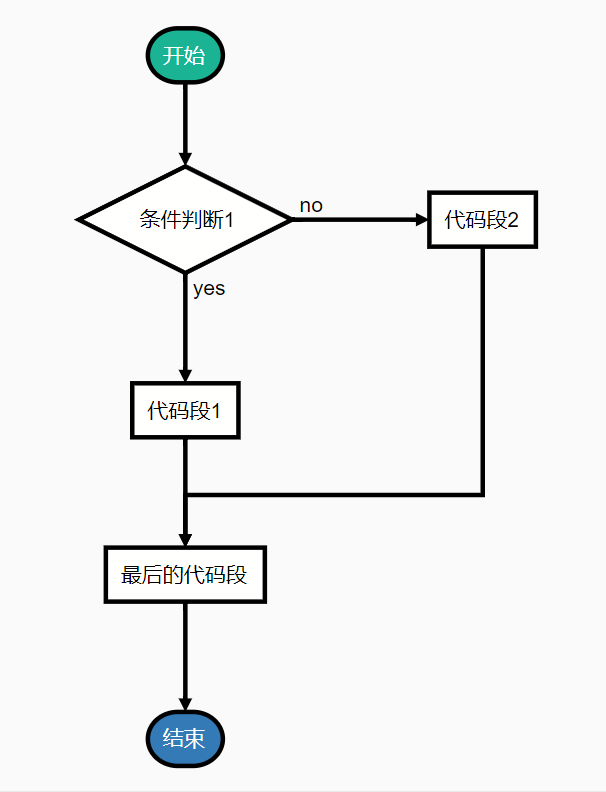
选择结构又叫分支结构。

顺序结构的程序虽然能解决计算、输出等问题，但不能做判断再选择。对于要先做判断再选择的问题就要使用选择结构。

选择结构的执行是依据一定的条件选择执行路径，而不是严格按照语句出现的物理顺序。选择结构的程序设计方法的关键在于构造合适的分支条件和分析程序流程，根据不同的程序流程选择适当的分支语句。

选择结构适合于带有逻辑或关系比较等条件判断的计算，设计这类程序时往往都要先绘制其程序流程图，然后根据程序流程写出源程序，这样做把程序设计分析与语言分开，使得问题简单化，易于理解。

女人给当程序猿的丈夫打电话：“下班顺路买一斤包子带回来，如果看到卖西瓜的，买一个。”当晚，程序猿手捧一个包子进了家门。。。

女人怒道：“你怎么就买了一个包子？！”答曰：“因为看到了卖西瓜的。

女人认为的流程：

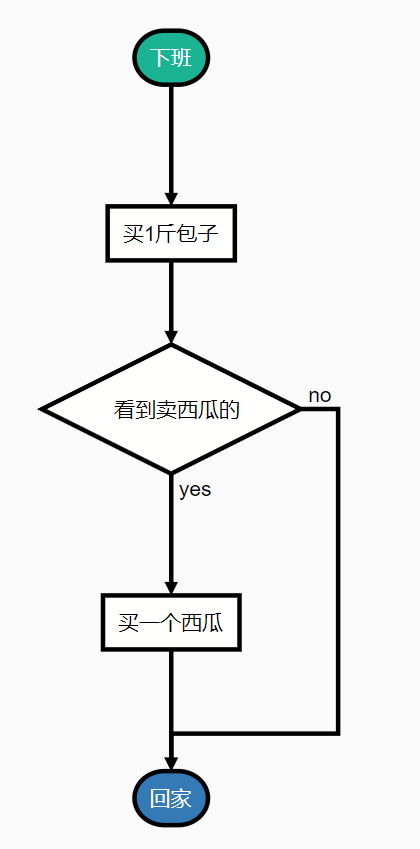
程序员以为的流程：

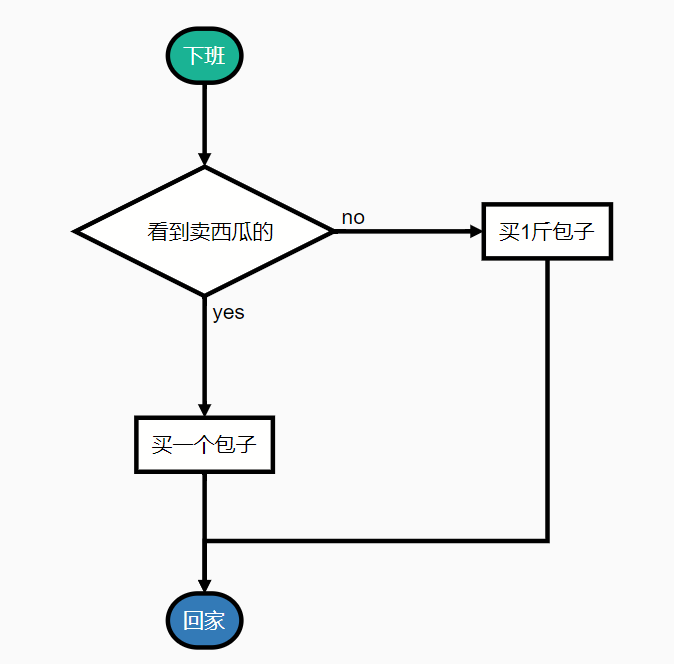
循环结构

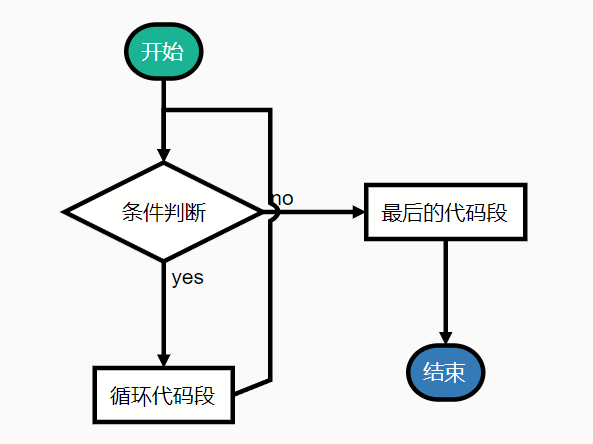
循环结构可以减少源程序重复书写的工作量，用来描述重复执行某段算法的问题，这是程序设计中最能发挥计算机特长的程序结构， C 语言中提供四种循环，即 goto 循环、 while 循环、 do … while 循环和 for 循环。

四种循环可以用来处理同一问题，一般情况下它们可以互相代替换，但一般不提倡用 goto 循环，因为强制改变程序的顺序经常会给程序的运行带来不可预料的错误，在学习中我们主要学习 while 、 do … while 、 for 三种循环。

常用的三种循环结构学习的重点在于弄清它们相同与不同之处，以便在不同场合下使用，这就要清楚三种循环的格式和执行顺序，将每种循环的流程图理解透彻后就会明白如何替换使用。

如将使用 while 循环的例题，用 for 语句重新编写一个程序，这样能更好地理解它们的作用。特别要注意在循环体内应包含趋于结束的语句（即循环变量值的改变），否则就可能成了一个死循环，这是初学者的一个常见错误。

单选题

判断：各种程序结构互不相关，彼此独立。

A. 对

B. 错

题解

B 选择结构和循环结构里面都包含有顺序结构，不彼此独立。

单选题

选择：（？）结构不可以单独存在、（？）结构可以单独存在

A、选择、顺序

B、选择、循环

C、循环、选择

题解

A 选择和循环结构不可以单独存在、顺序结构可以单独存在

代码段

上面的流程图中，多次提到代码段的概念，代码段简单来说就是花括号 {}{} 中间的部分。代码段中还可以包含其他的代码段。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    代码段的内容
}

习题

课堂练习:直角三角形面积

输入直角三角形直角边长a, b求三角形面积并输出。结果保证是整数。

输入格式

共一行：2个数a,b，对应直角三角形2个直角边的长度（1 <= a, b <= 1e9）

输出格式

输出这个直角三角形的面积。

输入样例

3 4

输出样例

6

数据范围

1 <= a, b <= 1e9

样例解释

3 * 4 / 2 = 6

#include <iostream>
using namespace std;
int main() {
  long long a, b;
  cin >> a >> b;
  cout << a * b / 2 << endl;
  return 0;
}

我们先来构思一下我们的程序：

(1) 声明 long long 类型变量 a,b ，因为 a,b 的取值范围为 1e9 ，因此他们的乘积可能达到 1e18 ，所以需要使用 long long 。

(2) 声明 long long 类型变量 c

(3) 读入 a,b(直角边长)

(4) 计算 a∗b/2 （直角三角形面积）并储存在变量 c 。

(5) 输出变量 c

（注：这个题目因为保证了结果为整数，所以不需要使用浮点型进行计算）

这恰恰是按照我们在程序中写出的相应代码的顺序执行的。

课后作业:高斯求和

德国著名数学家高斯幼年时代聪明过人，上学时，有一天老师出了一道题让同学们计算：

1＋2＋3＋4＋…＋99＋100＝？

老师出完题后，全班同学都在埋头计算，小高斯却很快算出答案等于 5050。高斯为什么算得又快又准呢？原来小高斯通过细心观察发现：

1＋100＝2＋99＝3＋98＝…＝49＋52＝50＋51。

1～100正好可以分成这样的50对数，每对数的和都相等。于是，小高斯把这道题巧算为（1+100）×100÷2＝5050。

输入格式

输入1个数n。(1 <= n <= 1000)

输出格式

输出 1+2+3+....n 的计算结果

输入样例

100

输出样例

5050

数据范围

对于20%的数据，x≤100； 对于100%的数据，x≤1000，x为正整数。

#include <iostream>
using namespace std;
int main() {
  long long n;
  cin >> n;
  cout << (1+n)*n/2 << endl;
  return 0;

}

利用题目中给出的公式，计算 1−>n 的和即可。

头脑风暴

蚂蚁爬杆问题

有一根细木杆，有几只蚂蚁。木杆很细，不能同时通过两只蚂蚁。开始时，蚂蚁朝左还是朝右是任意的，蚂蚁们只会朝前走或者调头，但不会后退。当任意两只蚂蚁碰头时，两只蚂蚁会同时调头朝反方向走。蚂蚁们每秒可以走一厘米的距离。

现在假设木杆长 27 厘米，木杆上有五只蚂蚁，分别在 3 厘米、 7 厘米、 11 厘米、 17 厘米、 23 厘米的位置，初始朝向是右、左、左、右、左。求第一只蚂蚁下杆的时间和最后一只蚂蚁下杆的时间？

因为所有蚂蚁都是相同的，每次蚂蚁碰撞后虽然都会掉头走，但如果以 2 个点的位置来描述 2 只碰撞后的蚂蚁的轨迹，会发现碰撞后的情况，同没有碰撞各自直走的轨迹是相同的。因此只要直接结算所有蚂蚁直走时下杆的时间就可以了，取其中的最大值。