L1-09 顺序结构

顺序结构的概念

顺序结构是程序中最简单的流程控制结构，没有特定的语法，程序运行时将按照代码的先后顺序依次执行，我们之前几个章节中接触过的代码大多是这样执行的。

单选题

循环结构和选择循环结构中一定包含（？）结构。

A. 顺序结构

B. 选择结构

C. 循环结构

题解

A

循环结构和选择循环结构中一定包含顺序结构

顺序结构流程图

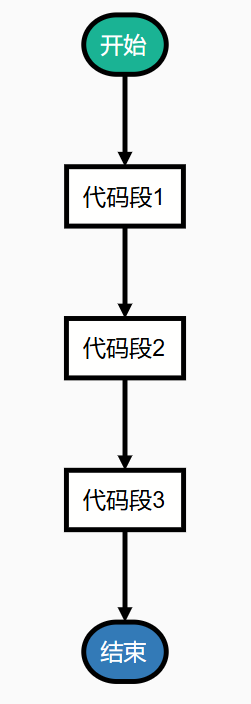
上面这张图即为一个简单的顺序结构程序的流程图。

所谓流程图就是用来表示程序运行步骤的示意图

从上图中我们可以很直观的感受顺序结构的概念，顺序结构就像是一张简单的安排表，按照时间顺序给出了要做的事情，对应在程序中就是按照要执行的顺序写出相应的语句。

2020 年 8 月，我国火箭军在西部某地发射中程弹道导弹成功命中南海某移动航母标靶。

发射弹道导弹打击航母流程大概包含：

• 点火发射

• 收到发射指令

• 回传数据给导弹

• 雷达跟踪搜寻目标

• 导弹不间断搜寻定位

• 命中摧毁航母标靶

  

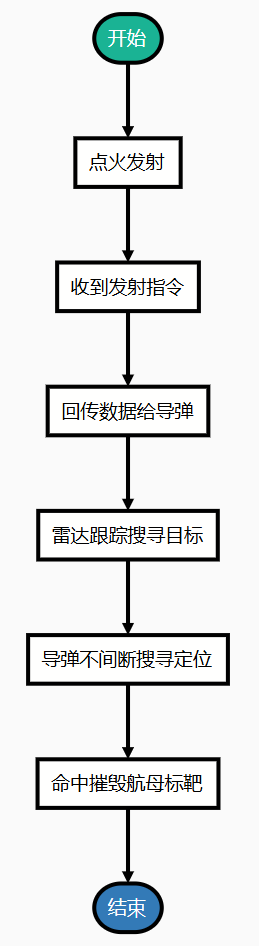
这是一个标准的顺序结构。

三变量交换法

在处理计算的过程中，我们经常需要交换两个变量的值。例如：

#include<bits/stdc++.h>
using namespace std;
int main() {
    int m = 5, n = 6;
    return 0;
}

交换 m,n 的值，如果直接交换：

#include<bits/stdc++.h>
using namespace std;
int main() {
    int m = 5, n = 6;
    m = n; //m = 6
    n = m; //n = 6, 5 丢失了
    cout << m << " " << n << endl;
    return 0;
}

6 6

我们会发现， m=5 丢失了。交换两个语句的顺序。

#include<bits/stdc++.h>
using namespace std;
int main() {
    int m = 5, n = 6;
    n = m; //n = 5
    m = n; //m = 5
    cout << m << " " << n << endl;
    return 0;
}

5 5

这时 n=6 丢失了。那么应该怎么办？

交换两个变量的值，首先我们可以将两个变量看作装有不同液体的两个瓶子，我们要调换他们的所装的液体，我们需要找一个空瓶子来辅助。这时候我们要做的事情就是：

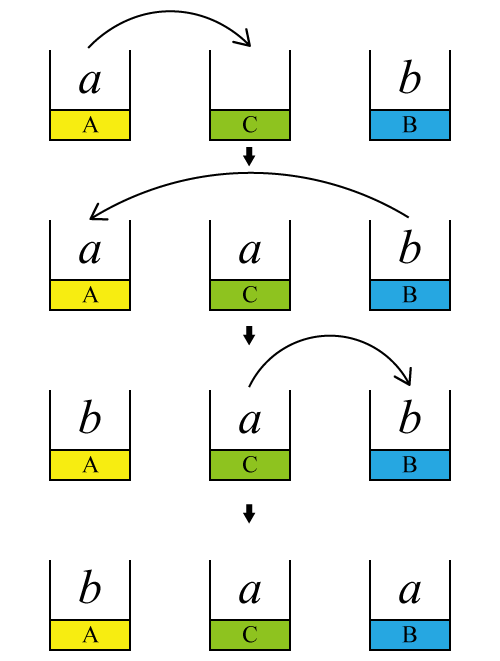
1、找到一个空瓶子 C

2、把 A 瓶子中的液体倒入 C 瓶子中

3、把 B 瓶子中的液体倒入 A 瓶子中

4、把 C 瓶子中的液体（原来 A 瓶子中的液体）倒入 B 瓶子

上面这样四步操作完，我们就实现了两个瓶子交换液体的操作。而交换两个变量的值，也是类似的操作，需要多借助一个变量来存储值。

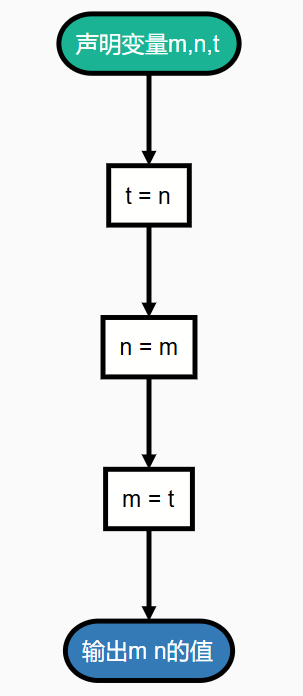
6 5

这就是 3 变量交换法。也是顺序结构的经典示例，对应的流程图如下：

填空题

5、下列编程语句的输出结果是：______

#include<bits/stdc++.h>
using namespace std;
int main() {
    int m = 5, n = 6;
    n = m;
    m = n;
    cout << m + n << endl;
    return 0;
}

题解

10

因为：m=5,n=6 n=m：把m的值5赋值给n得：n=5； m=n：把m的值5赋值给n得推出m=6； 所以得：m+n等于5+5等于10； 所以输出：10

单选题

int a = 4, b = 8; 下列哪组语句能实现变量 a 和 b 值互换（    ）

A. int t; a = t; b = a; t = b;

B. int t = a; a = b; b= t;

C. int t = a; b = t; a = b;

D. int t; a = b; b = a; t = a;

题解

B

a和b相互交换:int t = a; a = b; b= t;

单选题

我们已知交换 2 个变量的值需要 1 个额外的变量，这样总共用到 3 个变量，那么交换 8 个变量的值，最少需要总共多少个变量呢？

A. 9

B. 10

C. 11

D. 12

题解

A

1、无论是对几个变量进行交换、需要都至少交换的变量数目加1

课堂练习:启蒙练习-数字交换

编写程序读入三个数到整型变量a,b,c,将让a存储原本b中的值，让b存储原本c中的值， 让c存储原本a中的值，输出交换后a,b,c的值

输入格式

输入三个整数a,b,c，以空格隔开

输出格式

输出交换后的a,b,c，以空格隔开

输入样例

4 5 6

输出样例

5 6 4

数据范围

对于100%的数据，1≤a,b,c≤100

样例解释

原本a=4,b=5,c=6；

根据题意，需要让b的值赋给a，c的值赋给b，a的值赋给c。

因此最终结果中应为：a=5,b=6,c=4。

#include <bits/stdc++.h>
using namespace std;
int main() {
  int a, b, c;
  cin >> a >> b >> c;
  int t = a;
  a = b;
  b = c;
  c = t;
  cout << a << ' ' << b << ' ' << c << endl;
  return 0;
}

题解 1

可以直接利用上面的 3 变量交换法，先交换 a,b ，此时 b 中保存的是 a 的值，再交换 b,c 即可。

还有一个交换变量次数更少的方法：

t=a;a=b;b=c;c=t;

这是 3 变量交换法的扩展，利用这种方法交换 n 个变量，只需要 n+1 次赋值操作。

结语

看到最后读者也许会有这样的疑惑: 难道程序不都是按照在代码中写下的顺序执行的吗？

其实不然，除顺序结构外，选择结构和循环结构都有其特定的执行顺序，在选择结构中，尽管可能我们写下了很多语句，但程序在特定条件下只会执行特定的语句；在循环结构中，尽管我们只写了几句话，程序也可能会将这几句话按照特定的顺序不断执行任意次。

然而，尽管选择结构的功能强大，但在大多数程序中最基本的结构依然是顺序结构，选择结构和循环结构就像是武侠小说中各种武功秘籍。而顺序结构则是内力基础，只有将内力修炼好，修炼那些高深的武功秘籍才会得心应手。

习题

课后作业:线段的数量

一条直线上有n个点，请你求出共有多少条线段？

例如本题的图中，共包含AB,BC,AC这3条线段。

输入格式

输入一个整数n，表示直线上点的数量。（n<=10000）

输出格式

输出一个整数，表示线段的数量。

输入样例

3

输出样例

3

数据范围

对于 50% 的数据，1≤n≤100； 对于 100% 的数据，1≤n≤10000；

样例解释

对于样例中的情形，共包含AB,BC,AC这3条线段，因此答案为3。

#include <bits/stdc++.h>
using namespace std;
int main() {
  int n;
  cin >> n;
  cout << (1 + n - 1) \* (n - 1) / 2 << endl;
  return 0;
}

题解 1

对于含有 n 个点的直线，若我们将相邻两点所组成的线段称为“小线段”，那么样例中的 AB,BC 即是这种“小线段”。不难发现：

包含 1 个“小线段”的线段数量为 n−1 ；

包含 2 个“小线段”的线段数量为 n−2 ；

......

以此类推，直到包含 n−1 个“小线段”的线段数量为 1 ；

利用高斯求和，线段总数为：

$(n-1)+(n-2)+...+2+1={\displaystyle \frac{n\ast (n-1)}{2}}$