L1-12 循环结构初探

循环概述

什么是循环

循环结构是指在程序中需要反复执行某个功能而设置的一种程序结构。它由循环体中的条件，判断继续执行某个功能还是退出循环。根据判断条件，循环结构又可细分为以下两种形式：先判断后执行的循环结构和先执行后判断的循环结构。

单选题

想实现 1 到 200 之间所有数字的逐个相加，更适合选用以下哪个程序结构（ ）

A. 顺序结构

B. 选择结构

C. 倒序结构

D. 循环结构

题解

D

实现 1 到 200 之间所有数字的累加，更适合选用循环结构

循环的作用

之前我们曾经学习过输出 Hello World 。如果我们需要输出 10 个 Hello World ，应该怎么办？

cout << "Hello World" << endl;
cout << "Hello World" << endl;
cout << "Hello World" << endl;
......
cout << "Hello World" << endl; //写10遍

那么，如果要输出 100 个呢？

循环可以帮我们有效的解决这个问题。减少重复的工作量。循环是程序设计中最能发挥计算机特长的程序结构 。循环结构可以看成是一个条件判断语句和一个向回转向语句的组合。

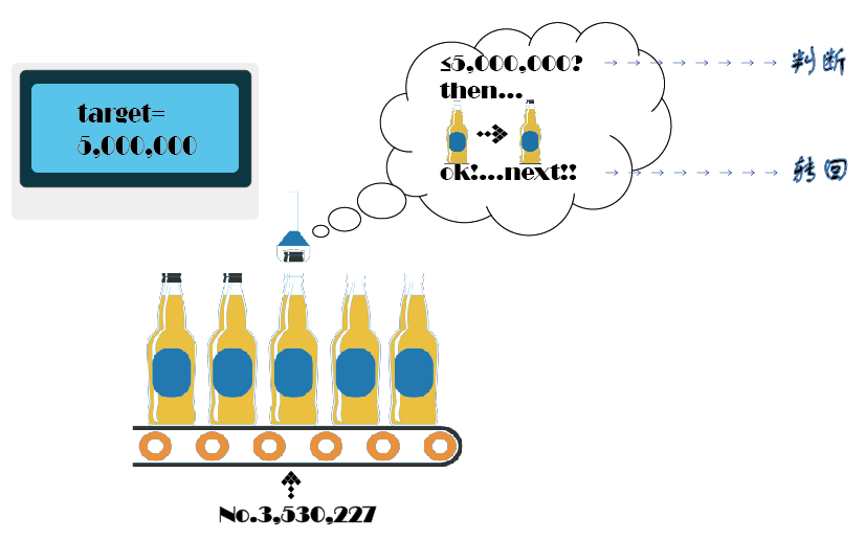
循环结构

循环的流程

循环结构的流程图如下：

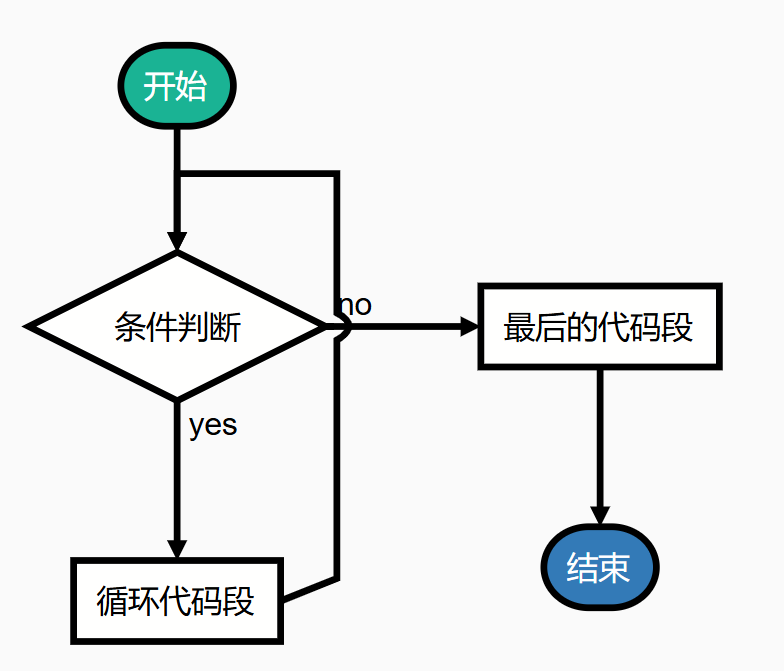
这个流程图如果比较抽象的话，你可以想象一下你在吃薯片，只要袋子还有薯片，你就会去抓来吃，直到薯片吃完，吃薯片这个动作不断重复，这就是循环。

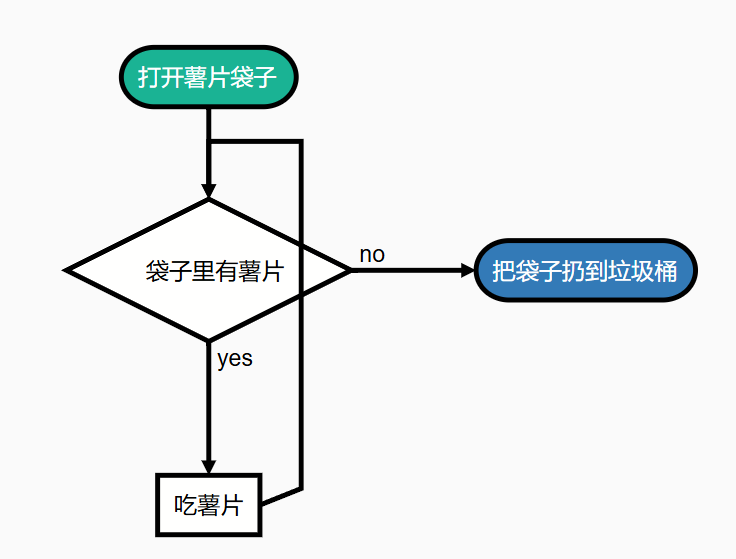
循环条件

循环条件是一个表达式，在计算机中，逻辑表达式只有两个值，真和假，或者说 true 和 false （即 1 和 0 ），但是如果将一般表达式作为循环条件的判断语句的话，那么非零值为真，零值为假。

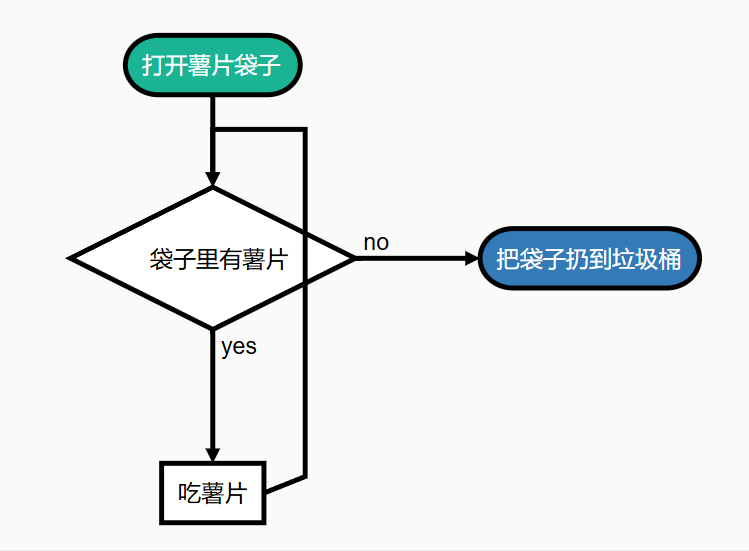
循环体

循环体就是被重复的内容。它可以是一个语句，一个表达式，复杂点的话还可以是一个循环，一个代码段，所以循环是可以嵌套的。当然，循环体也可以什么都不做，为空的语句，在逻辑上以及语法上都是合法的，虽然一般没有特别的意义。

在薯片的例子中，吃薯片，就是循环体（循环代码段）。

单选题

判断：循环体可以是一个语句，一个表达式，也可以是空的语句。 （ ）

A. 对

B. 错

题解

对

判断：循环体可以是一个语句，一个表达式，也可以是空的语句

C/C++中的循环结构

C++ 语言中提供四种循环，即 ：

1. for 循环
2. while 循环
3. do…while 循环
4. goto 循环

四种循环可以用来处理同一问题，一般情况下它们可以互相代替换，但一般不提倡用 goto 循环，因为强制改变程序的顺序经常会给程序的运行带来不可预料的错误，在学习中我们主要学习 for 、 while 、 do⋯while 三种循环。

常用的三种循环结构学习的重点在于弄清它们相同与不同之处，以便在不同场合下使用。这就要清楚三种循环的格式和执行顺序，将每种循环的流程图理解透彻后就会明白如何替换使用，如把 while 循环的例题，用 for 语句重新编写一个程序，这样能更好地理解它们的作用。特别要注意在循环体内应包含趋于结束的语句（即循环变量值的改变），否则就可能成了一个死循环，这是初学者的一个常见错误。

在学完这三个循环后，应明确它们的异同点：

用 while 和 do ⋯ while 循环时，循环变量的初始化的操作应在循环体之前，而 for 循环一般在语句中进行的。

while 循环和 for 循环都是先判断表达式，后执行循环体。

而 do ⋯ while 循环是先执行循环体后判断表达式，也就是说 do ⋯ while 的循环体最少被执行一次，而 while 循环和 for 就可能一次都不执行。

另外还要注意的是这三种循环都可以用 break 语句跳出循环，用 continue 语句结束本次循环，而 goto 语句与 if 构成的循环，是不能用 break 和 continue 语句进行控制的。

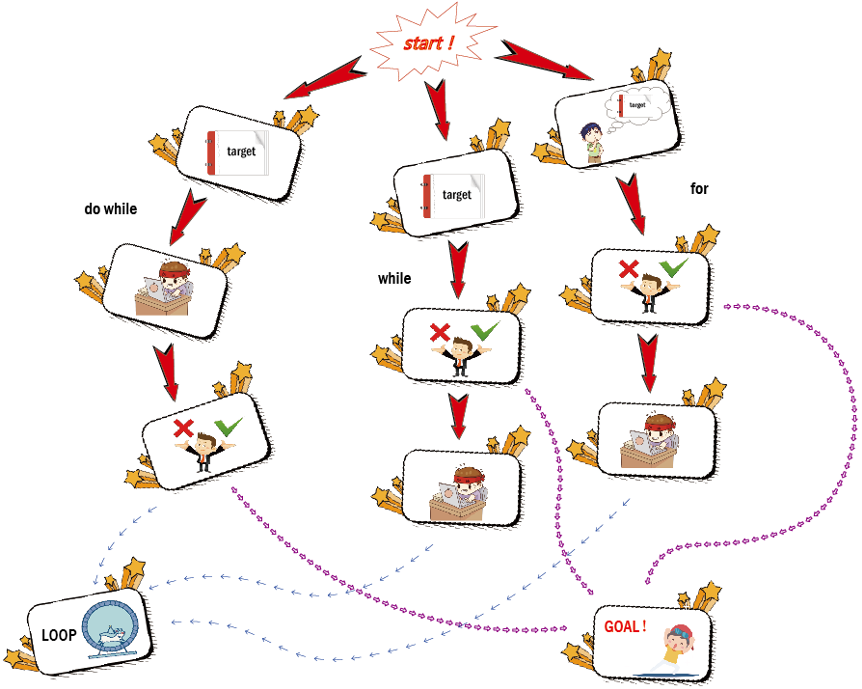
顺序结构、分支结构和循环结构并不彼此孤立的，在循环中可以有分支、顺序结构，分支中也可以有循环、顺序结构，其实不管哪种结构，我们均可广义的把它们看成一个语句。在实际编程过程中常将这三种结构相互结合以实现各种算法，设计出相应程序。

单选题

循环体可以不使用{ }。

A. 对

B. 错

题解

A

当循环体只有一条语句的时候可以不使用大括号

死循环

如果循环的判断条件永远为真（永真值），例如： 1=1 。那么循环便永远不会有结束的时候，此时我们称之为死循环。

单选题

while(1){ cout<<"你好"<<endl; } 这个会是一个死循环 （ ）

A. 对

B. 错

题解

对

while(1)其中1代表一个常量表达式，它永远不会等于0。 循环会一直执行下去。除非你设置break等类似的跳出循环语句循环才会中止

习题

课堂练习:Hello 51nod

51nod平台新推出了在线代码调试功能，于是夹克姥爷想让你仿照 Hello World 写一段演示代码。

具体的，给出一个正整数n，请你输出n次"Hello 51nod!"。

输入格式

输入一个正整数n。

输出格式

输出n行，每行一个"Hello 51nod!"。

输入样例

2

输出样例

Hello 51nod!
Hello 51nod!

#include <bits/stdc++.h>
using namespace std;
int main() {
  int n;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cout << "Hello 51nod!" << endl;
  }
  return 0;
}

课后作业:启蒙练习-顺序输出

给出两个正整数 a 和 b（其中a<b），请你由小到大输出从a到b的每个正整数。

输入格式

输入两个正整数a,b，以空格隔开。

输出格式

输出共b-a+1行，每行包含一个题意要求的正整数。

输入样例

5 8

输出样例

5
6
7
8

数据范围

对于100%的数据，1≤a<b≤200。

#include <bits/stdc++.h>
using namespace std;
int main() {
  int a, b;
  cin >> a >>  b;
  for (int i = a; i <= b; i++) {
    cout << i << endl;
  }
  return 0;
}

自行理解题目图片中的代码的意义，照抄并提交运行即可。以下为 for 循环的代码实现。

头脑风暴

正方形的数量

一个 m×n 的方格图，有多少个不同的正方形。

例如： 4×3 的方格图中共有 20 个正方形，其中：

正方形大小	正方形数量
1×1	12 个
2×2	6 个
3×3	2 个

我们假定 $m>=n$ 。那么：

边长为 $1$ 的正方形数量为： $m\times n$ 个。

边长为 $2$ 的正方形数量为： $(m-1)\times (n-1)$ 个。

......

边长为 $n$ 的正方形数量为： $(m-n+1)\times 1$ 个。

所以最终的结果为：

$mn+(m-1)(n-1)+(m-2)(n-2)+...2(m-n+2)+(m-n+1)$

如何能够快速的计算上面的式子呢？

对于每一项，我们将其划分为两部分， $n^2,(m-n)n$ 。因为 $n^2+(m-n)n=mn$ 所以式子变为：

$(n^2+(m-n)n)+((n-1{)}^2+(m-n)(n-1))+((n-2{)}^2+(m-n)(n-2))+...(1^2+(m-n))$

把这个式子整理一下，得到：

$\begin{array}{c}{n}^2+(n-1{)}^2+\dots 2^2+1^2+(m-n)(1+2+3+\dots n)=\\ n^2+(n-1{)}^2+\dots 2^2+1^2+(m-n)n(n+1)/2=\\ (2n+1)n(n+1)/6+(m-n)n(n+1)/2\end{array}$

最后一步，利用了平方和公式： $(1-n)$ 的平方和等于 $(2n+1)n(n+1)/6$ 。